La práctica de estos juegos te pueden ayudar a mantener la mente activa, a mejorar la observación, atención y concentración y en general proporciona un mayor bienestar.
TORRE DE HANOI
Las Torres de Hanoi es un juego
matemático que consiste en tres varillas verticales y un número indeterminado
de discos que determinarán la complejidad de la solución. No hay dos discos
iguales, están colocados de mayor a menor en una varilla ascendentemente, y no
se puede colocar ningún disco mayor sobre uno menor a él en ningún momento. El
juego consiste en pasar todos los discos a otra varilla colocados de mayor a
menor ascendentemente.
Leyenda: Dios al crear el mundo, colocó
tres varillas de diamante con 64 discos en la primera. También creó un
monasterio con monjes, los cuales tienen la tarea de resolver esta Torre de
Hanoi divina. El día que estos monjes consigan terminar el juego, el mundo
acabará. El mínimo número de movimientos que se necesita para resolver este
problema es de 264-1. Si los monjes hicieran un movimiento por segundo, los 64
discos estarían en la tercera varilla en poco menos de 585 mil millones de
años. Como comparación para ver la magnitud de esta cifra, la Tierra tiene como
5 mil millones de años, y el Universo entre 15 y 20 mil millones de años de
antigüedad, sólo una pequeña fracción de esa cifra.
Resolución: el problema de las Torres
de Hanoi es curioso porque su solución es muy rápida de calcular, pero el
número de pasos para resolverlo crece exponencialmente conforme aumenta el
número de discos. Para obtener la solución más corta, es necesario mover el
disco más pequeño en todos los pasos impares, mientras que en los pasos pares
sólo existe un movimiento posible que no lo incluye. El problema se reduce a
decidir en cada paso impar a cuál de las dos pilas posibles se desplazará el
disco pequeño:
El algoritmo en cuestión depende del número de
discos del problema.
Si inicialmente se tiene un número impar de
discos, el primer movimiento debe ser colocar el disco más pequeño en la pila
destino, y en cada paso impar se le mueve a la siguiente pila a su izquierda (o
a la pila destino, si está en la pila origen).
La secuencia será DESTINO, AUXILIAR, ORIGEN,
DESTINO, AUXILIAR, ORIGEN, etc.
Si se tiene inicialmente un número par de
discos, el primer movimiento debe ser colocar el disco más pequeño en la pila
auxiliar, y en cada paso impar se le mueve a la siguiente pila a su derecha (o
a la pila origen, si está en la pila destino).
La secuencia será AUXILIAR, DESTINO, ORIGEN,
AUXILIAR, DESTINO, ORIGEN, etc.
KAKURO
En cada fila y en cada columna hay que
rellenar las casillas vacías con números del 1 al 9, sin que estos se repitan.
Además, las suma de estos números (por fila o por columna) tiene que ser igual
al número clave dado. El número clave superior indica la suma de su fila y el
número clave inferior la suma de su columna.
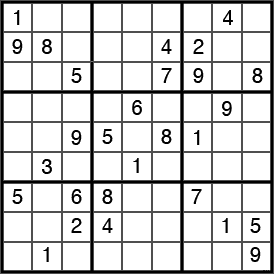
SODOKU
Tienes que rellenar con los números del uno al
nueve (sin repetir ninguno) las casillas que conforman cada fila, cada columna
y cada celda



No hay comentarios:
Publicar un comentario